Jun 12, 18 · 三角関数を使って三角形の面積を求める sinを利用して、三角形の高さを求めて、 そこから三角形の面積を求めます。 なので、2辺の長さとその間の角度が分かっていれば、三角形の面積を求めることができます。 下図をみてください。 点BからACに向けてヘロンの公式(代数的証明)幾何的証明はこちら 三角形の三辺の長さ a,b,c が分かっているとき、三角形の面積Sは、 とヘロン三角形の面積は2の倍数である ことの別証明らしきものを投稿させて下さい。御批正を頂きたく宜しくお願い致します。 ヘロン三角形で、3辺の辺長を a、b、c とし、その半周長を s 、面積を S と
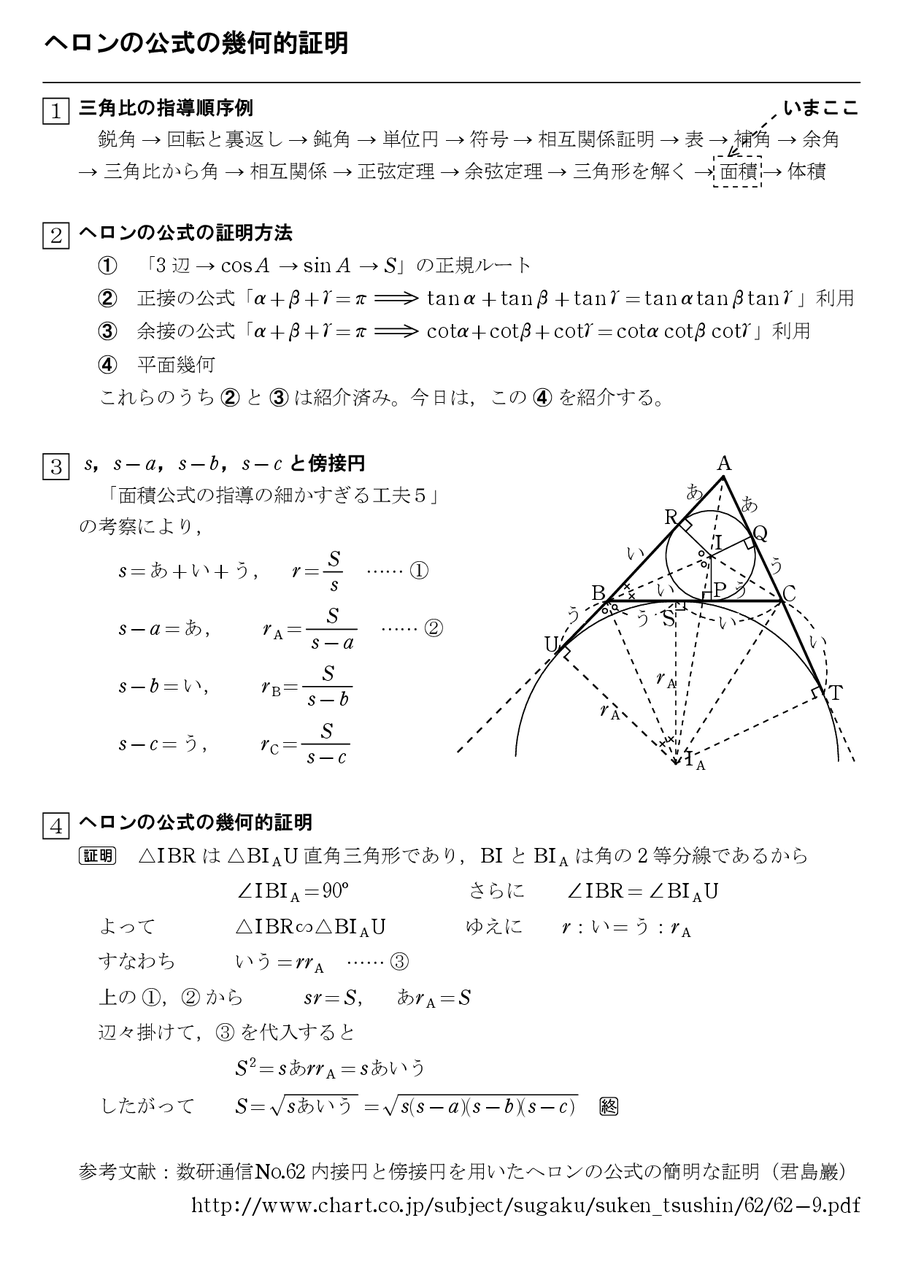
ヘロンの公式の幾何的証明 怜悧玲瓏 高校数学を天空から俯瞰する
ヘロンの公式 証明 簡単
ヘロンの公式 証明 簡単-ヘロンの公式の証明 では、なぜこのような公式で面積を求めることができるのか。 その証明方法について確認しておきましょう。 証明はちょっと複雑な式変形を伴います。 オレは公式が使えたらそれでヘロンの公式の証明(三角関数を使わずに) ヘロンの公式 は任意の 三角形 の3辺 a, b, c の長さから 面積S を求める公式である。




ヘロンの公式の幾何的証明 怜悧玲瓏 高校数学を天空から俯瞰する
明もある.しかしながら,ヘロン自身によるヘロンの公式の証明はなかなか目にすることはない.この証明を みるとヘロンの豊かな才能と同時に,初等幾何の限界のようなものを感じざるを得ない. 証明4abc の面積をs とする.またその内接円をo とし式です。まずは、ヘロンの公式を覚えてください。 ヘロンの公式 3辺の長さがBC = a;CA = b;AB = c である4ABC でs = a b c 2 とする。 このとき4ABC の面積S はS = p s(s a)(s b)(s c) である。 (ヘロンの公式の証明は問題の後ろに書いてあります。デジタル大辞泉 ヘロンの公式の用語解説 三角形の面積Sを3辺の長さa・b・cから求める公式。3辺の和の半分をsとすると、S2=s(s-a)(s-b)(s-c)で与えられる。古代ギリシャの数学者・技術者ヘロン(Heron)によるが、ニュートンが再発見した。
前回 https//wwwyoutubecom/watch?v=6MBwzRYm4&index=18&list=PLKRhhk0lEyzOfDE8u9U0GWX3aa43XeMOr 次回 https//wwwyoutubecom/watch?v=cSbY6lb4fng&indexヘロンの公式において, この隠された関係が公式が正しいことを示す上で最もエレガントな方法です。 回答の1番下にヘロンオリジナルの幾何を使ってこの関係を証明しますが, まずは色のついたそれぞれの三角形のペアを並び替えることで x y z の和がこの三角形の面積に等しいことを示させFeb 28, 16 · ご指摘に感謝したい。なお、√程度ならヘロンの公式を導く 途中の計算式を使えば簡単に計算できるらしいことを知った。 さて、ヘロンの公式であるが、その証明は余り扱わない。インターネットの「ヘロンの公式の証明」で検索すると、いっ
Nov , 19 · ヘロンの公式とその証明(数1) ヘロンの公式とその証明(数1) Watch later Share Copy link Info Shopping Tap to unmute If playback doesn't begin shortlyヘロンの公式 三角形の面積を求めるときに用いたヘロンの公式を紹介します。 <証明> 使用する公式 ・三角関数の基本公式 sin 2 Acos 2 A=1 ・余弦定理 a 2 =b 2 c 22bccosA b 2 =c 2 a 22cacosB c 2 =a 2 b 22abcosC ・三角形の面積の公式(面積をSとする) S= 余弦定理のMathAquarium定理・公式の証明三角形の面積(ヘロンの公式) 1 三角形の面積 ABC において,頂点A,B,C における角の大きさ をA,B,C,その対辺BC,CA,AB の長さをそれぞれ a,b,c,面積をS とすると,次の等式が成り立つ。 S= 2 1 bc sinA= 2 1 ca sinB= 2 1 ab



09 2 Dfrac6272 dfra Descubre Como Resolverlo En Qanda




複素数 Wikipedia
Mar 06, 21 · ヘロンの公式の証明 図のように三角形 A B C ABC A BC の内心を I I I , I I I から各辺へ下ろした垂線の足をそれぞれ P , Q , R P,Q,R P , Q , R とおく。 同じ点から引いた2本の接線の長さは等May 18, · ヘロンの公式は、三角形の3辺の長さから面積を求めるための公式です。 なぜ3辺の長さから面積が求められるのでしょうか? そもそも三角形の面積は「底辺 × 高さ ÷ 2」なので、高さがわからなければ面積もわからないのではないのでしょうか?ヘロンの公式を思い出し手計算を行いこのサイトで確認してみました。 a=103 b=635 c=425 で3615程度になるはずが6315というおかしな計算結果になるのはなぜでしょうか ?



新基礎数学 改訂版 大日本図書




ヘロンの公式の幾何的証明 怜悧玲瓏 高校数学を天空から俯瞰する
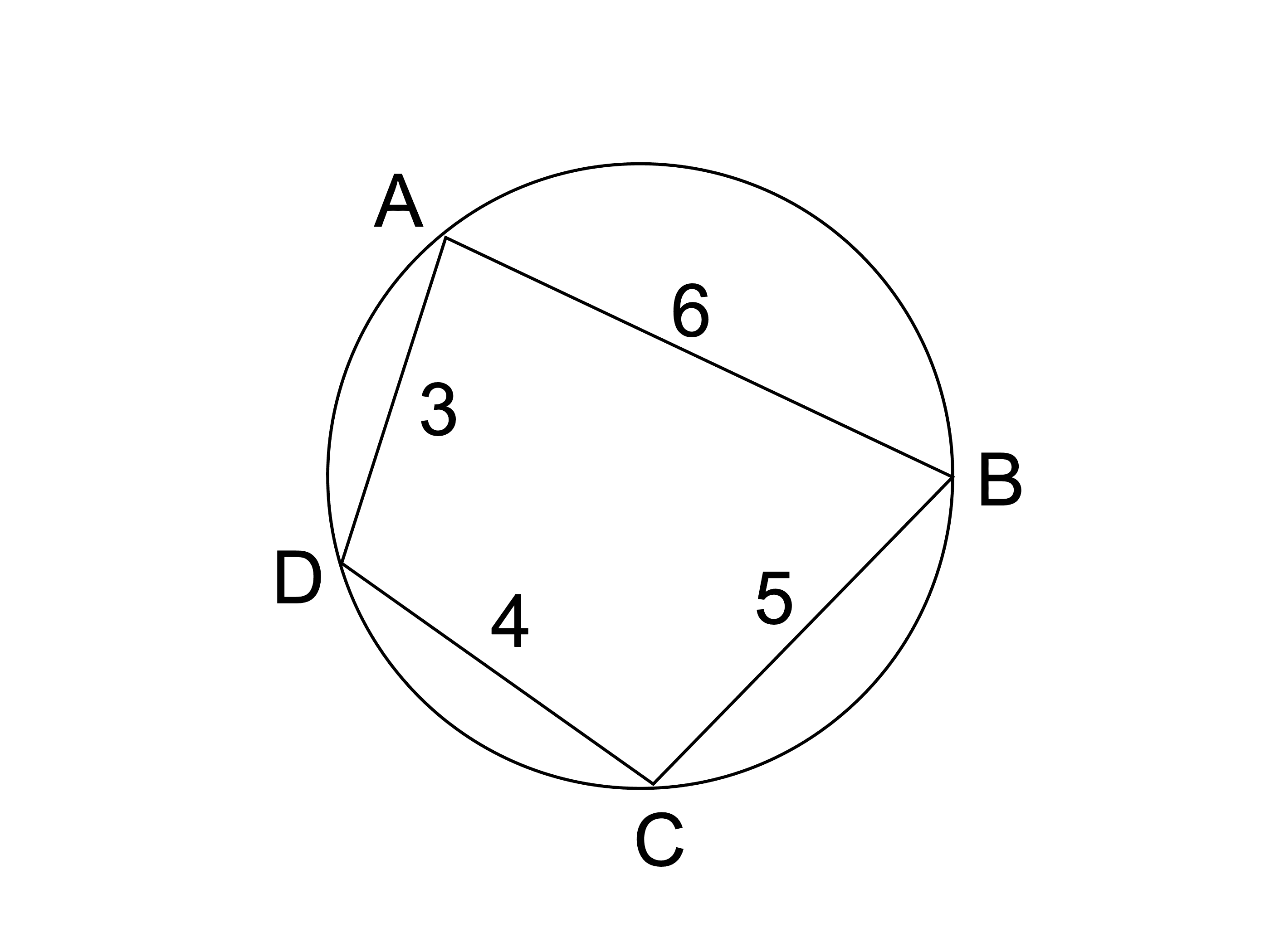
ヘロンの公式の証明です。 関連 余弦定理(前提知識) https//youtube/mz9iYmIyx_A About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety HowMar 06, 21 · つまり,ブラーマグプタの公式はヘロンの公式を含んでいると言えます。 以下では,ブラーマグプタの公式の証明を2つ紹介します。1つ目は三角関数を用いた素直な方法,2つ目はヘロンの公式による方法です。May 24, · ヘロンの公式の使用例 ヘロンの公式は 3辺の長さがわかっている三角形なら必ず面積が求められる 公式です。 しかし、3辺がわかっているからといって必ずしもこの公式を使うのが一番いいわけではありません。




ヘロンの公式とは ヘロンの公式の証明と使い方 演習問題付き Himokuri



三角形の面積の公式 京極一樹の数学塾
Feb 19, 21 · この記事では、「ヘロンの公式」やその証明について解説していきます。 また、四角形バージョンのブラーマグプタの公式についてもわかりやすく説明していくので、ぜひこの記事を通してマスターしてくださいね! 目次ヘロンの公式とヘロンの公式を用いた証明 方針: 不等式を三角形の各辺の長さ a , b , c a, b, c a , b , c のみで表してから3変数の不等式を代数的に証明する, というのが幾何不等式証明のもっとも基本的なパターンです。ヘロンの公式を証明 三角形の三辺さえ分かっていれば面積が求まるという、非常に面白いヘロンの公式ですが、 「なぜ、ヘロンの公式は成り立つのでしょうか?」 最後に、ヘロンの公式を証明してみま




ヘロンの公式で三角形の面積を求める 三辺の長さがわかっているときはコレ 数学の面白いこと 役に立つことをまとめたサイト



三角形とは 面積公式 角度 辺の長さ 重心 比の計算 受験辞典
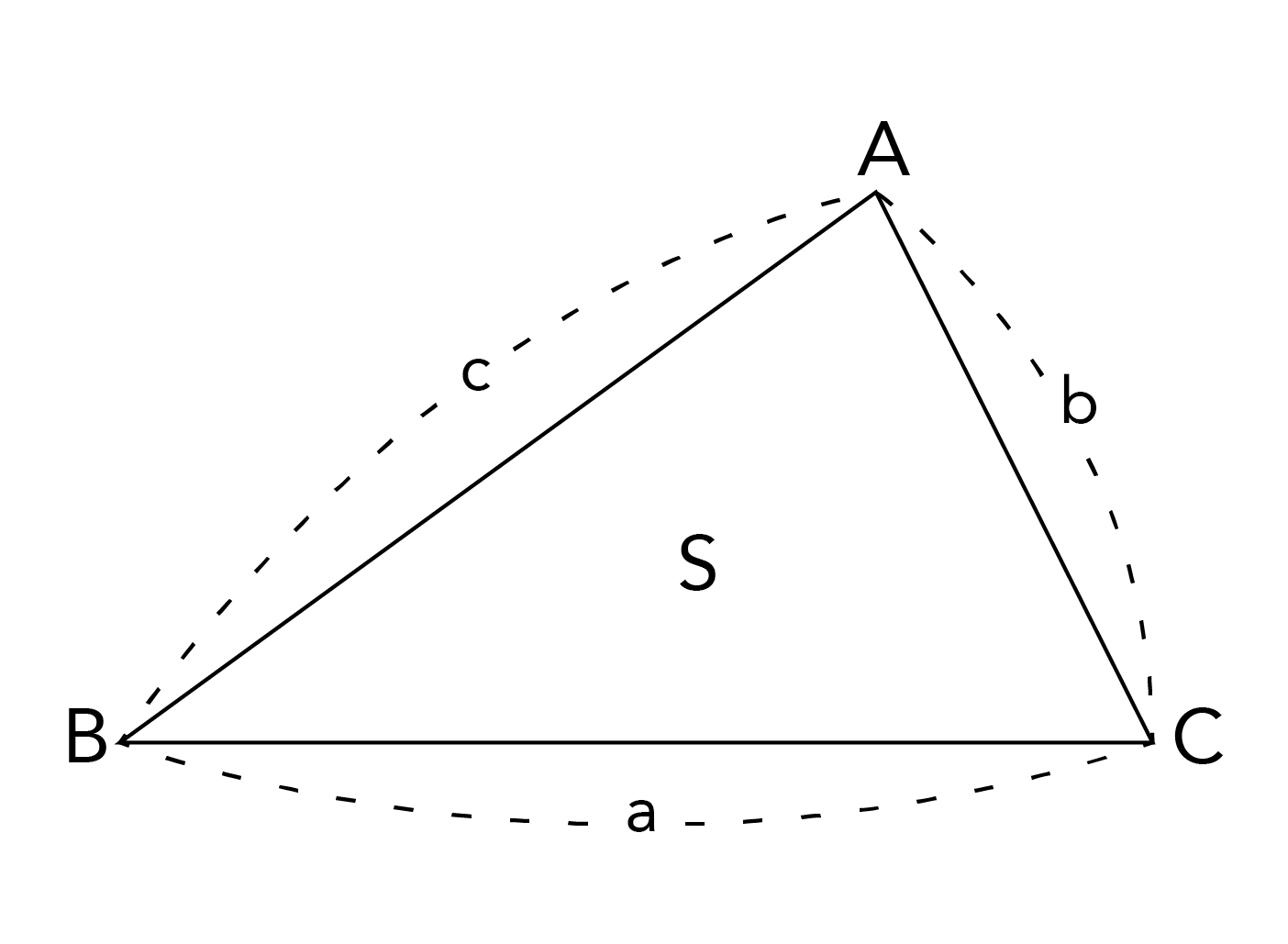
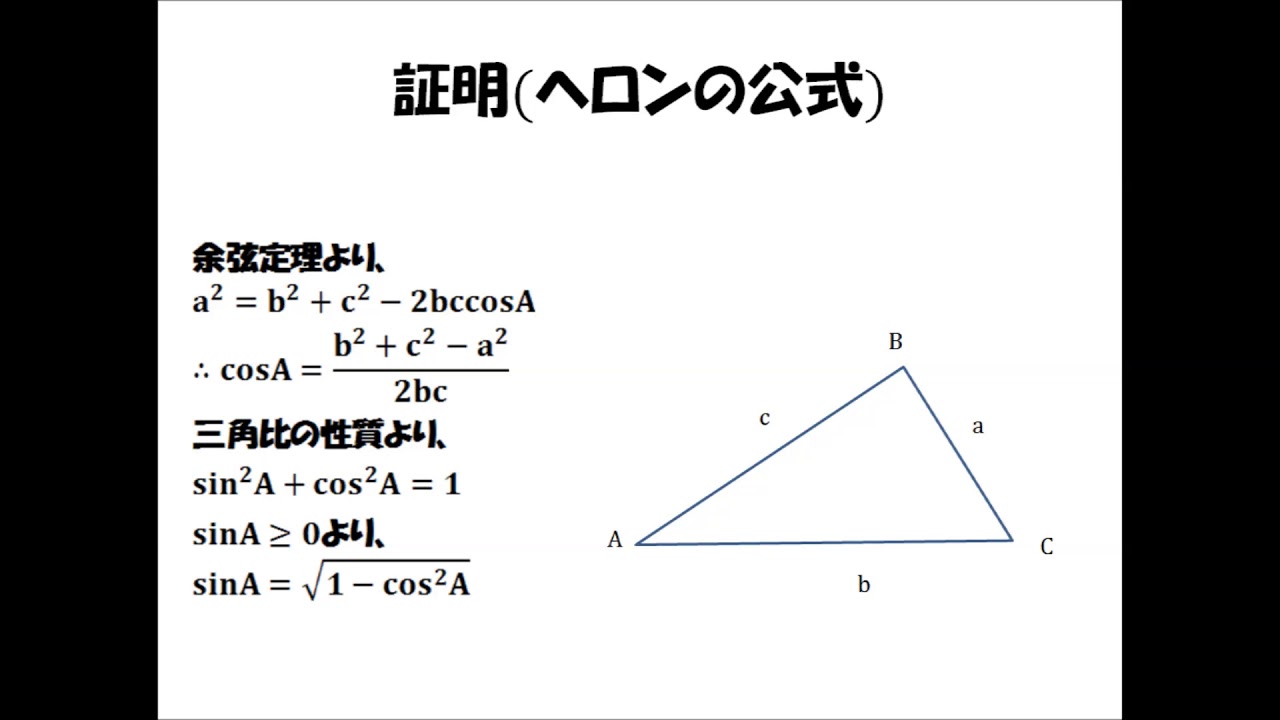
ヘロンの公式の部屋 ヘロンの公式(幾何的証明)代数的証明はこちら 三角形の三辺の長さ a,b,c が分かっているとき、三角形の面積Sは、 と表せる。 以下の説明では、左図のように、頂点および角度をA,B,Cで表し 各頂点に向かい合う辺の長さを、a,b,c で表します。 予備知識1(内接円に関する性質) ABCの内接円の各接点から頂点までの長さは下図の通り。 AEFeb 22, 17 · ヘロンの公式の使いどころ ヘロンの公式は必ずしも覚えていなければならない公式ではありません.なぜなら,三角形の三辺の長さが与えられた時,三角形の面積はヘロンの公式を用いなくても三角比を使えば求められるからです.実際,上の証明中にみヘロンの公式の証明 ではこの公式を証明していきましょう。 ABCにおいて、 余弦定理 より"a²=b²+c²−2b・c・cosA"なので ー① 続いて sin²A+cosA²=1 "の公式より これに①を代入すると ここで" a+b+c=2s "とすると、 b+c−a=a+b+c−2a=2s−2a=2 (s−a) ー② a−b+c=a+b+c−2b=2s−2b=2 (s−b) ー③




ヘロン の 公式 Excel エクセルでヘロンの公式により三角形の面積を求める方法 計算




17年08月24日 東大合格コム
Feb 06, 21 · 1 ヘロンの公式とは 2 ヘロンの公式の証明 21 三角形の面積は「底辺×高さ÷2」で求められる 22 三角形の高さは「斜辺×sinθ」で求められる (cos/sinの活用) 23 cosθは三辺の長さから求められる (余弦定理) 24 sinθは定理を使えば簡単にcosθに変換できる 25Aug 11, 19 · 紀元前1世紀末、エジプト人数学者であるヘロンが著書の中でこの公式の証明の1つを発表したため、アラブの数学者たちが彼の名前を公式に付け、「ヘロンの公式」が誕生した。ヘロンはギリシャ文化とバビロニア文化に精通した知識人であり、数学の中でも特に幾何分野に関して業績を残した人物である。Sep 06, 15 · へロンの公式へロンの公式は、3辺が既知の三角形の面積\(s\)を求める公式ですが、これは高校で学びますから、公式自体は覚えている方も多いと思います。しかしながら、ヘロンの公式を証明してくださいと言われると、あるいはこのような問題がでたら、できる人は限られるのではな




高校数学でよく使う三角形の面積公式まとめ おいしい数学



ヘロンの公式とは 証明や 四角形版 ブラーマグプタの公式 も 受験辞典
三角形の面積 3辺の長さがa,b,cの三角形の面積を求めるには、Aから辺BCへ垂線をたらし、その足をHとしてAH=hとおきます。 ABCの面積は ですが、ahをa,b,cだけの式に直すと、ヘロンの公式となります。 図で、h 2 =c 2 x 2 =b 2 (ax) 2 、従って c 2 x 2 =b 2 a 2 2axx 2 から となります。 すると より 4a 2 h 2 =4a 2 c 2 (c 2 a 2 b 2) 2 = (2acc 2 a 2 b 2 ) (2acc 2 a 2 b 2 )=ヘロンの公式の証明 三角比相互の関係 (平方関係)より sin 2 θ + cos 2 θ = 1 (1) 公式(1)を変形して、因数分解すると sin 2 A + cos 2 A = 1 sin 2 A = 1 - cos 2 A = ( 1+ cos A ) ( 1- cos A ) ( 2 ) 余弦定理より a 2 = b 2 c 2 2bc cos A ( 3 )(再追記) 例6.において、ヘロンの公式の初等的証明を示したが、次のような証明がある ことを最近知った。 ヘロンの公式における s-a、s-b、s-c の意味が分かって、思わず唸って しまった。




ヘロンの公式 東大合格コム




発展講座 トレミーの定理の使い方と証明 南数英指導会 南ノートブログ版
だから、 ヘロンの公式を使うのは3辺とも整数のとき 、と思っておいてもらって大丈夫です。 このヘロン公式を使うと、普通に三角形の面積を求めるよりもかなり速く求めることができます。 今回はプリントの後半で、ヘロンの公式の証明をしてあります。Jan 29, 21 · 中学数学 数学 高校数学 中学数学で出来る! ヘロンの公式の証明 21年2月3日 ヘロンの公式は、三角形の3辺の長さから面積を求める公式です 以下の三角形ABCの面積Sは S = s ( s − a) ( s − b) ( s − c) ( s = a b c 2) 今回は、この公式の「三角関数を使って証明する方法」と「中学数学だけで証明する方法」の2種類の証明方法を紹介していきますヘロンの公式 計算機が見つからず、手計算でやるかと思いましたが、検索してありました。 助かりました。 単一三角では便利ではありますが、通常舗装面積等は多くの三角形に集合体になります。 入力欄を増やす事は出来ませんでしょうか。 尚且つ




ヘロンの公式 計算を工夫して証明 今週の定理 公式no 4 Youtube




三角形の高さを求める 3つの方法 Wikihow
Sep 24, · この公式を用いて、ヘロンの公式を証明します。 まず、余弦定理により、 $$\cos{A}=\frac{b^2c^2a^2}{2bc}$$ となります。 余弦定理については、下の記事に詳しくまとめS = √s(s− a)(s−b)(s−c) ただし s = a b c 2 S = s (s − a) (s − b) (s − c) ただし s = a b c 2 それでは、この 公式の導出方法 と、 ヘロンの公式を使った計算例 について、見ていきましょう。
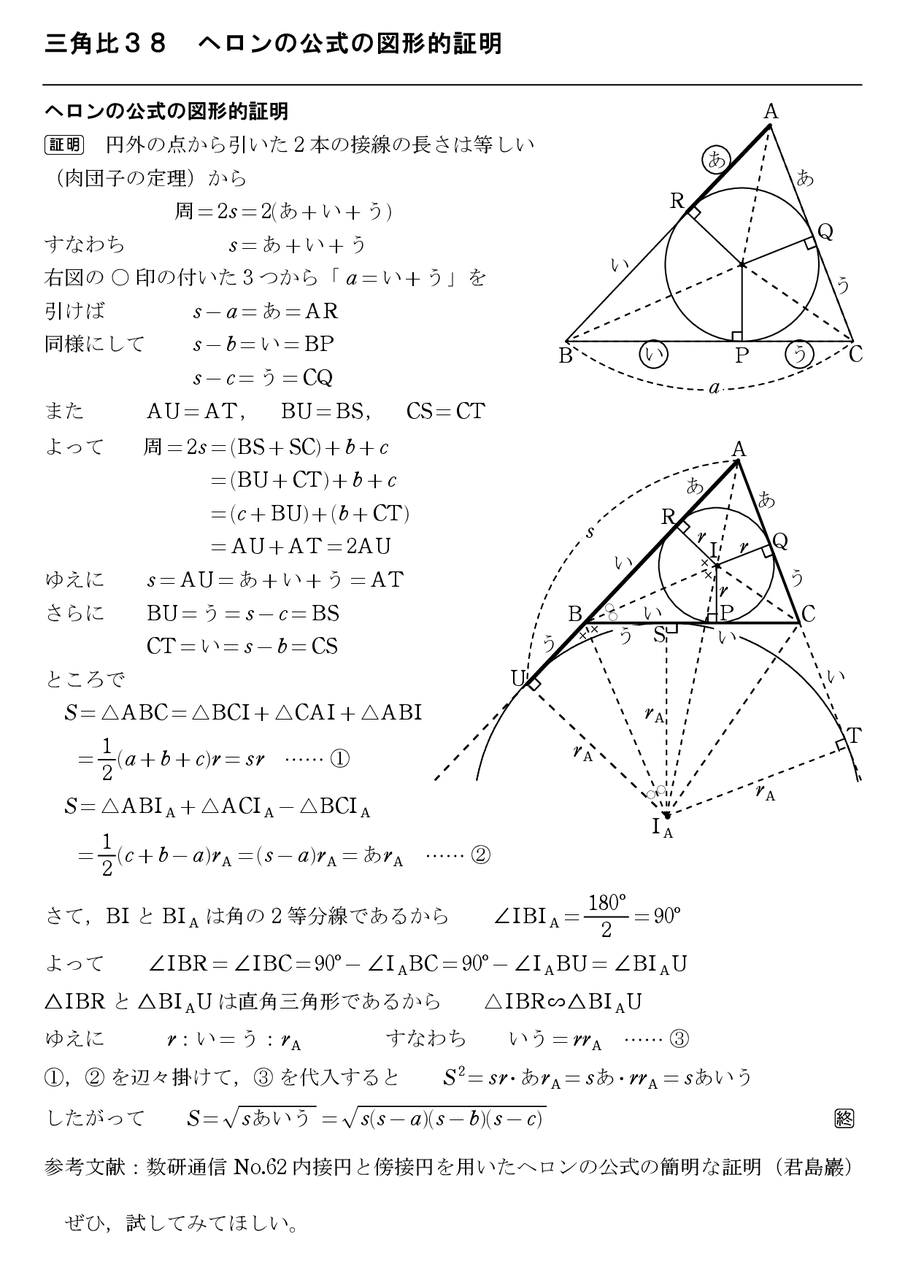



三角比38 ヘロンの公式の図形的証明 怜悧玲瓏 高校数学を天空から俯瞰する




オイラーの不等式 数 学 者 の 思ひ




数学の図形の問題です どうしても分からないので教えてい頂きたいです Clear




Haruka先生の数学証明シリーズ ヘロンの公式 中学レベル Youtube




メルカリ 東京都立高校入試 共通問題 受験数学 平面図形制覇 Vもぎ手書き解説 参考書 500 中古や未使用のフリマ




三角関数 はじめの一歩 勉強法のバイブル 帝都大学へのビジョン




北大の過去問で1文字固定法に関する問題の解説など 高校数学の達人 河見賢司のメルマガ 2018年9月18日 高校数学の勉強法 河見賢司のサイト




高校数学 因数分解 3乗が登場する因数分解の解き方をわかりやすく解説 数学の面白いこと 役に立つことをまとめたサイト




三角形の内接円の半径の求め方 公式 練習問題付き 理系ラボ




発展講座 メネラウスの定理の証明とその応用 南数英指導会 南ノートブログ版
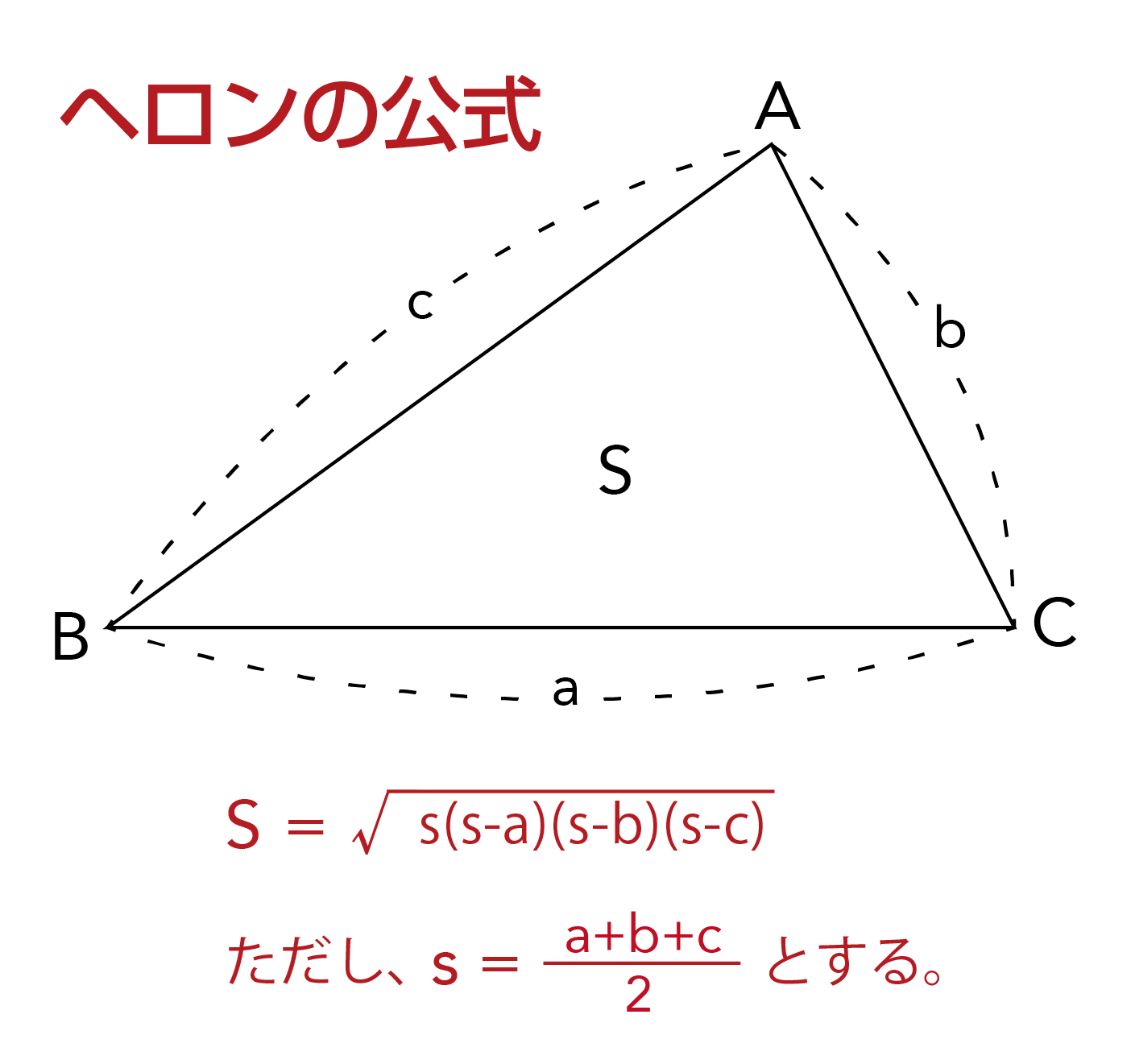



ヘロンの公式が一目でわかる 見やすい図で慶應生が解説 高校生向け受験応援メディア 受験のミカタ




高校数学b 三角形の面積のベクトル表示 成分表示とその証明 受験の月




Senior High数学的 高校数学 三角比 公式証明の旅 筆記 Clear




ヘロンの公式の証明 導出 を徹底解説 5分でわかる Youtube




ヘロン の 公式



011 7 49 大学受験完全個別指導予備校 実力養成会 The Ability Training School 実力養成会について 学習システム 費用 ニュース ブログ 実力養成会を選んだ理由 実力養成会の考え方 講師紹介 実績 よくあるご質問 ニュース ブログ ホーム ニュース




美しい公式 ヘロンの公式は 共通テストで狙われるかも でもそうでないとしてもこれは簡単すぎて美しすぎる公式だと思います 学習村の 国公立へ行こう




三辺の長さが与えられた三角形の面積を求めるヘロンの公式の別証明 身勝手な主張
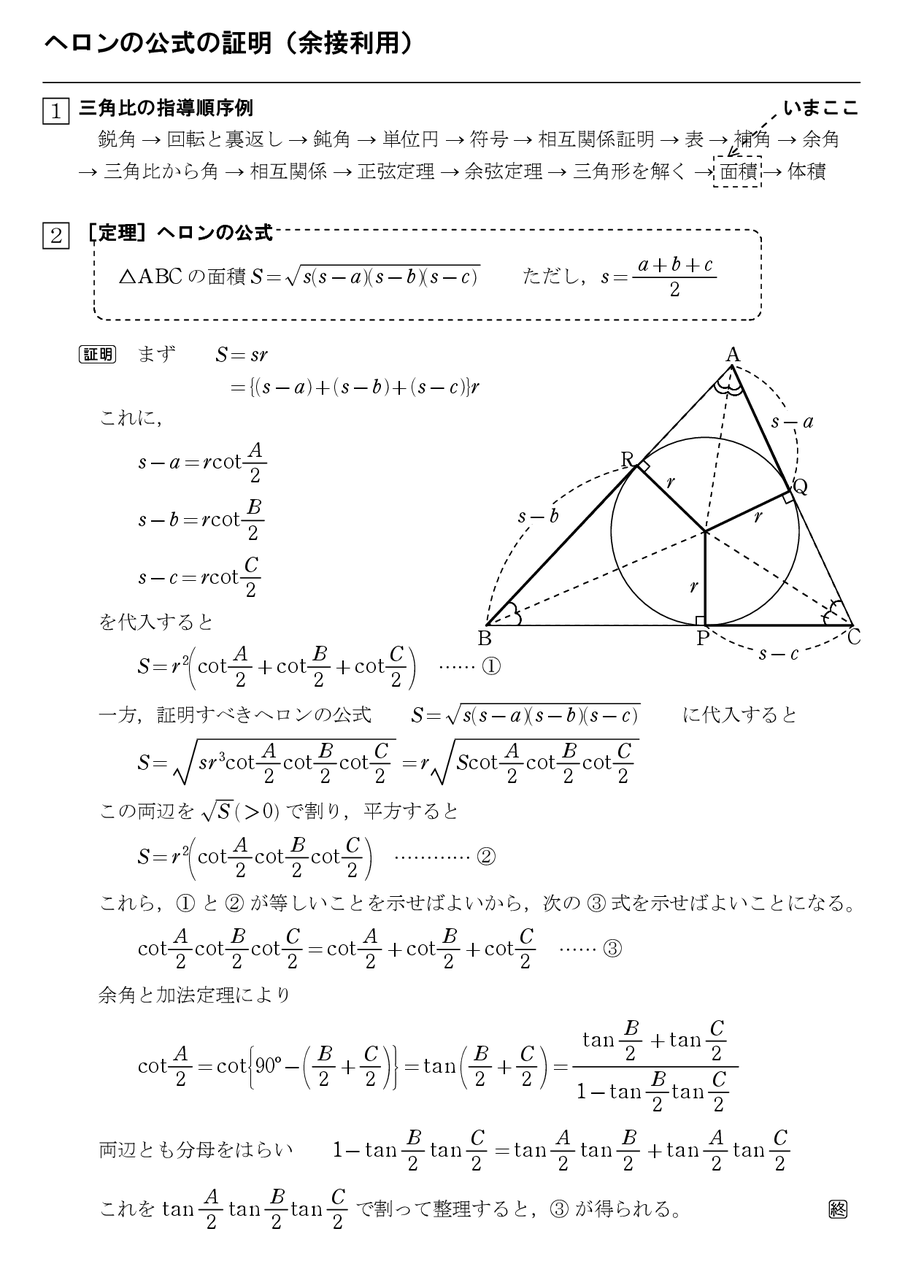



ヘロンの公式の証明 余接利用 怜悧玲瓏 高校数学を天空から俯瞰する
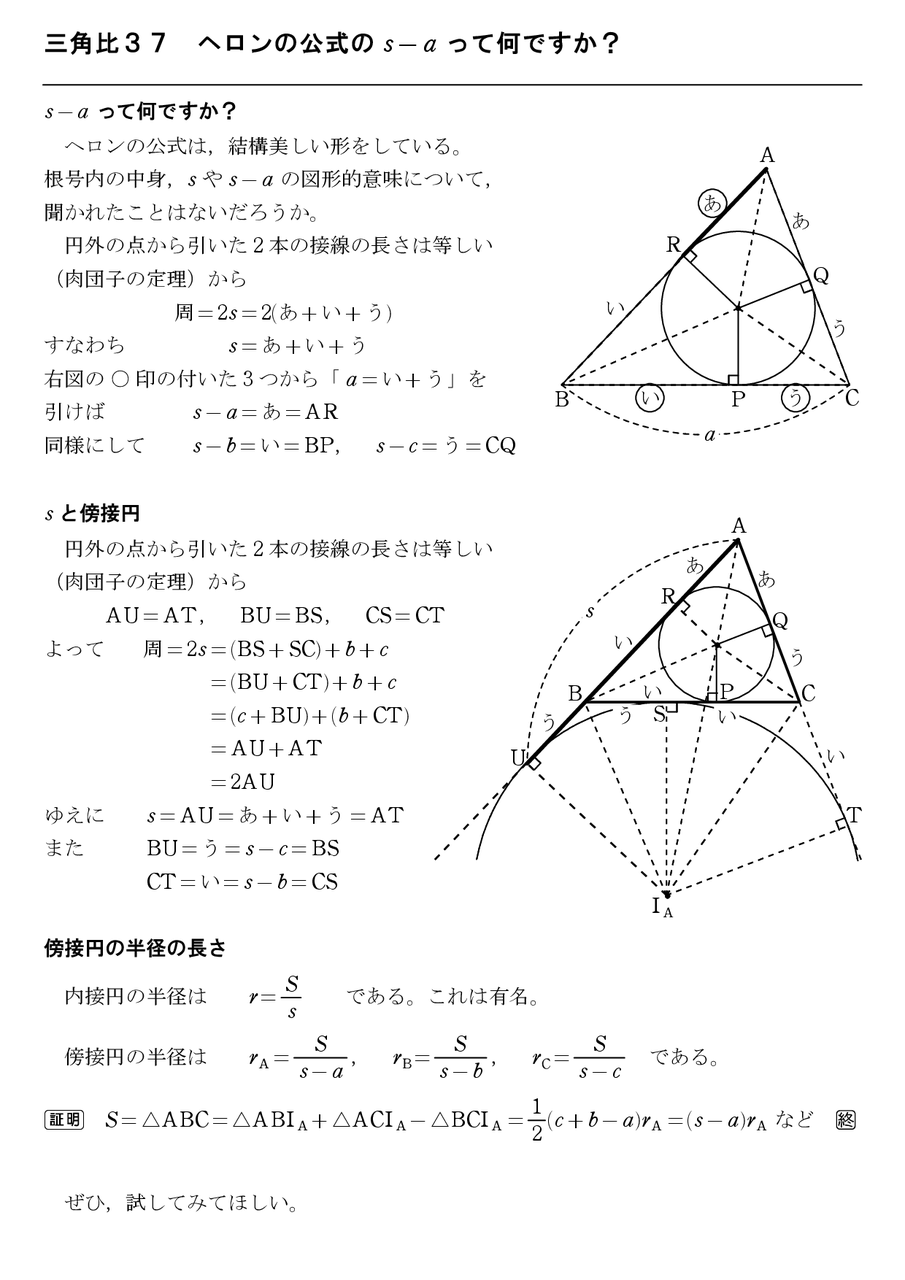



三角比38 ヘロンの公式の図形的証明 怜悧玲瓏 高校数学を天空から俯瞰する




先生 仮




三角比 Hashtag Videos On Tiktok




完全版 三角形の面積求め方一覧 高校生 数学のノート Clear
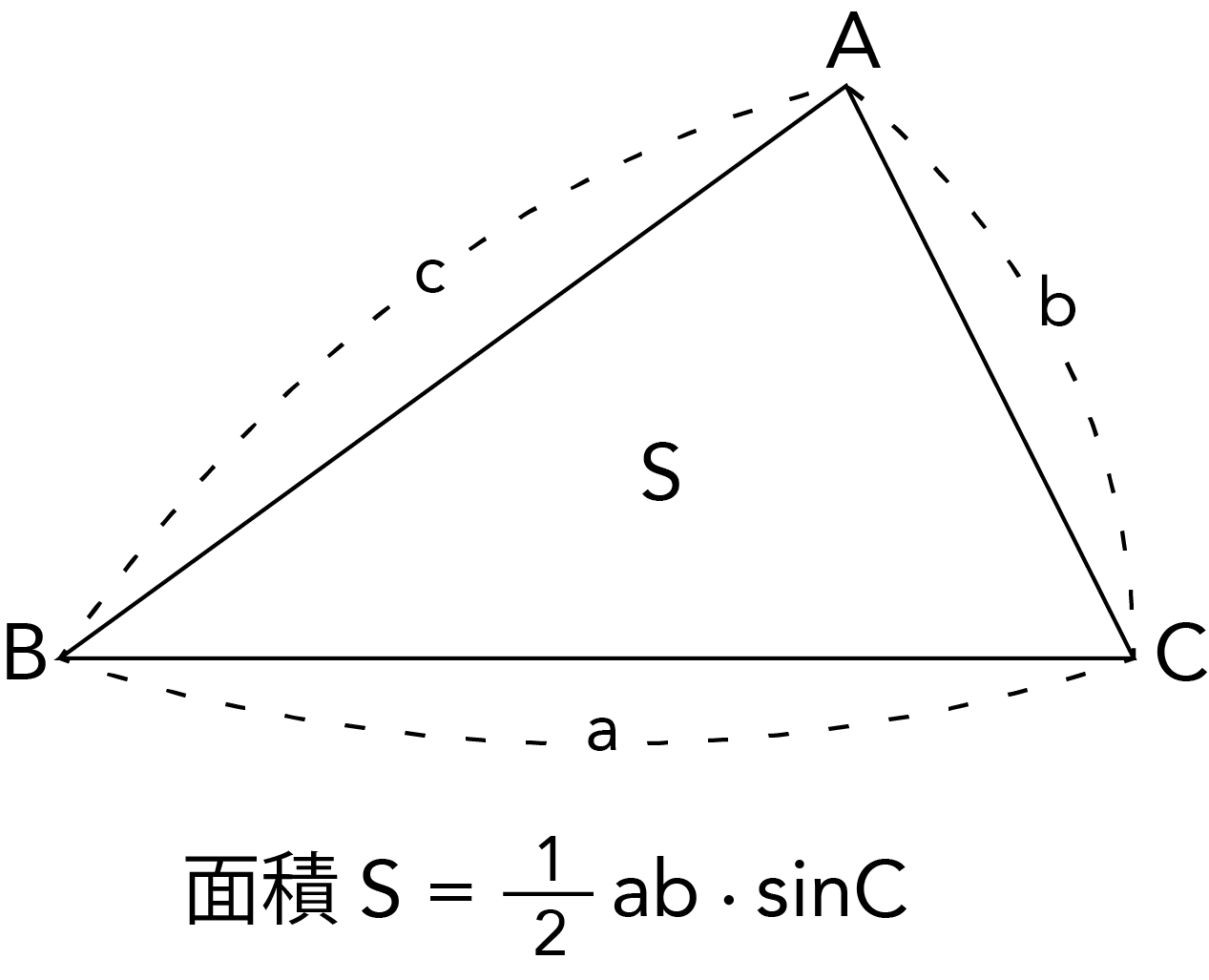



ヘロンの公式が一目でわかる 見やすい図で慶應生が解説 高校生向け受験応援メディア 受験のミカタ




三角比の添削 追記9月14日 Matsu Math Note
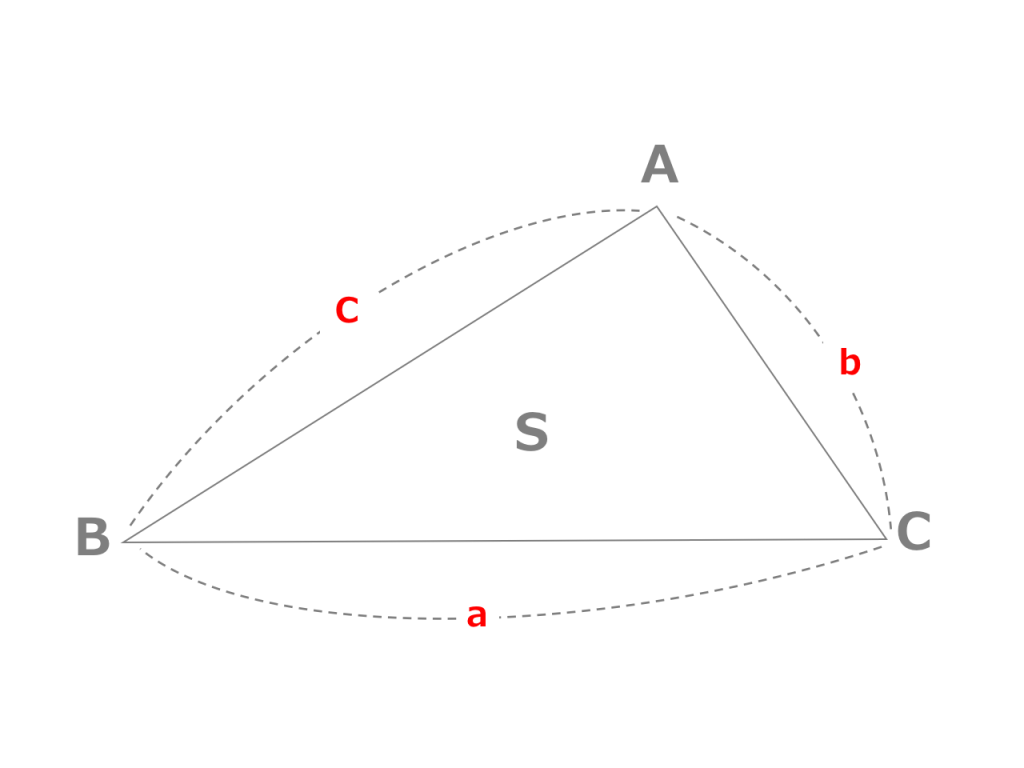



3分で分かる ヘロンの公式 証明と問題の解き方をわかりやすく 合格サプリ




ブラーマグプタの公式 東大合格コム




ヘロンの公式 を使って面積を求める方法 証明あり ますますmathが好きになる 魔法の数学ノート
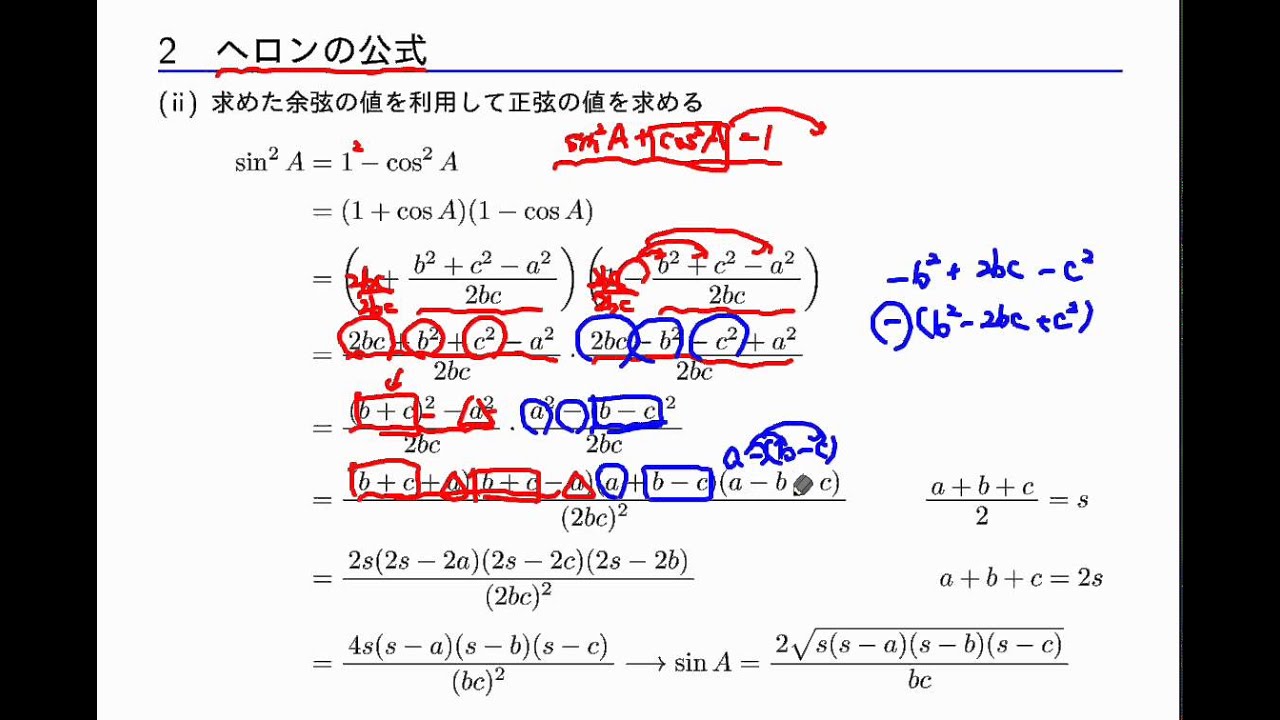



ヘロンの公式 まなびの学園




石松拓人 ちょっと前に 3辺の和が19の三角形の面積の最大値を求めよ って問題見た気がするんだけど ヘロンの公式を使わずにエレガントな解法思い付いたから見て ってかこれで証明になってる 数学クラスタの人




数学教材サンプル ジャズピアニスト若井優也のブログ




17年08月 東大合格コム




二等辺三角形の内接円 外接円に関する問題 2019年度前期日程の岡山大学文系の入試問題 身勝手な主張




高校数学 三角形の外接円の半径 内接円の半径と面積の関係 S 1 2r A B C 受験の月




ヘロンの公式の幾何的証明 怜悧玲瓏 高校数学を天空から俯瞰する




無料ダウンロード底辺高さ2 証明 最高のぬりえ




中学生版 ヘロンの公式 三平方の定理が楽に計算できる方法 Youtube



三角形の定理 公式の中で 最もマイナーなものは何ですか Quora




ヘロンの公式



ヘロンの公式が一目でわかる 見やすい図で慶應生が解説 高校生向け受験応援メディア 受験のミカタ



Images Of ブラーマグプタの公式 Japaneseclass Jp




正弦定理公式




本には載せなかった第7話 早稲田大学の入試問題より ヘロンの公式の証明 の別解です 花結び




ヘロンの公式の幾何的証明 怜悧玲瓏 高校数学を天空から俯瞰する




トップ100図形 の 公式 最高のぬりえ



史上最強図解 これならわかる 三角関数 ナツメ社




美しい公式 ヘロンの公式は 共通テストで狙われるかも でもそうでないとしてもこれは簡単すぎて美しすぎる公式だと思います 学習村の 国公立へ行こう



Haruka先生の数学証明シリーズ ヘロンの公式 Youtube
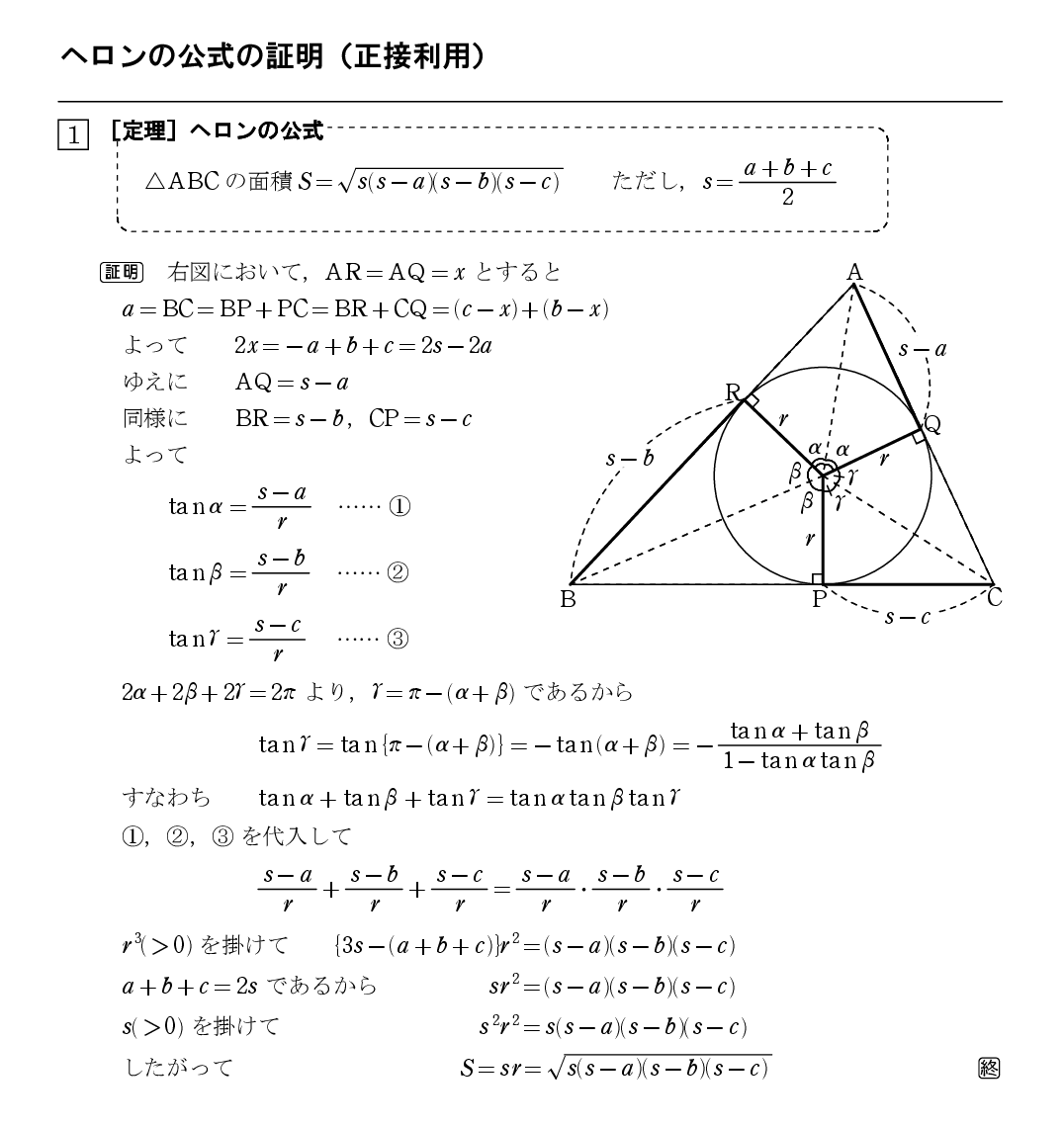



授業での雑談ネタ 18 ヘロンの公式の有名でない証明 怜悧玲瓏 高校数学を天空から俯瞰する



011 7 49 大学受験完全個別指導予備校 実力養成会 The Ability Training School 実力養成会について 学習システム 費用 ニュース ブログ 実力養成会を選んだ理由 実力養成会の考え方 講師紹介 実績 よくあるご質問 ニュース ブログ ホーム ニュース




高校数学 三角形の面積のヘロンの公式s S S A S B S C の証明と利用 受験の月
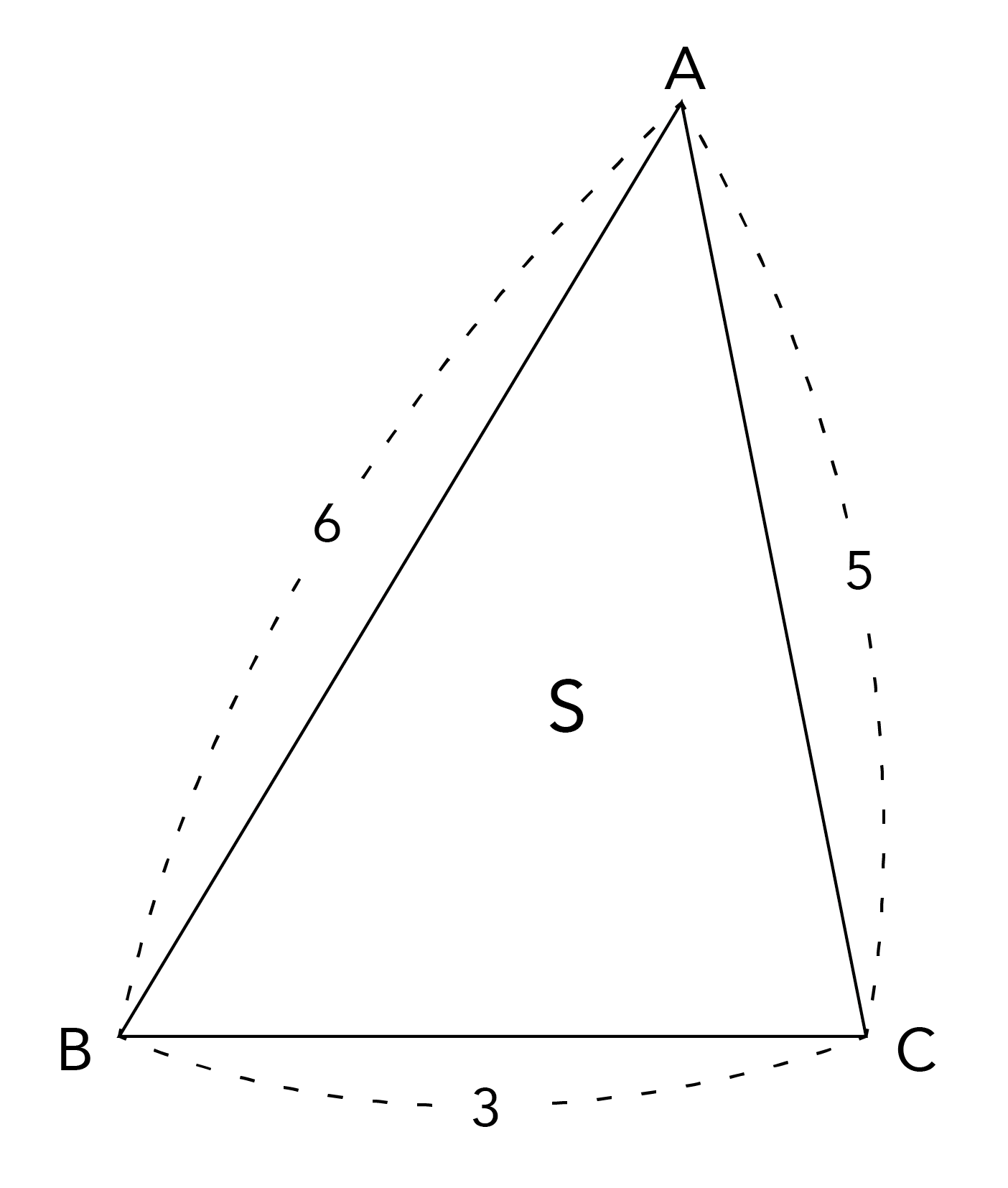



ヘロンの公式が一目でわかる 見やすい図で慶應生が解説 高校生向け受験応援メディア 受験のミカタ




18 受験で使える 三角形の面積公式シリーズ 医学生gの数学ノート




数学1 A編 完全攻略 高校数学の公式全部まとめてみたwww Cupuasu クプアス
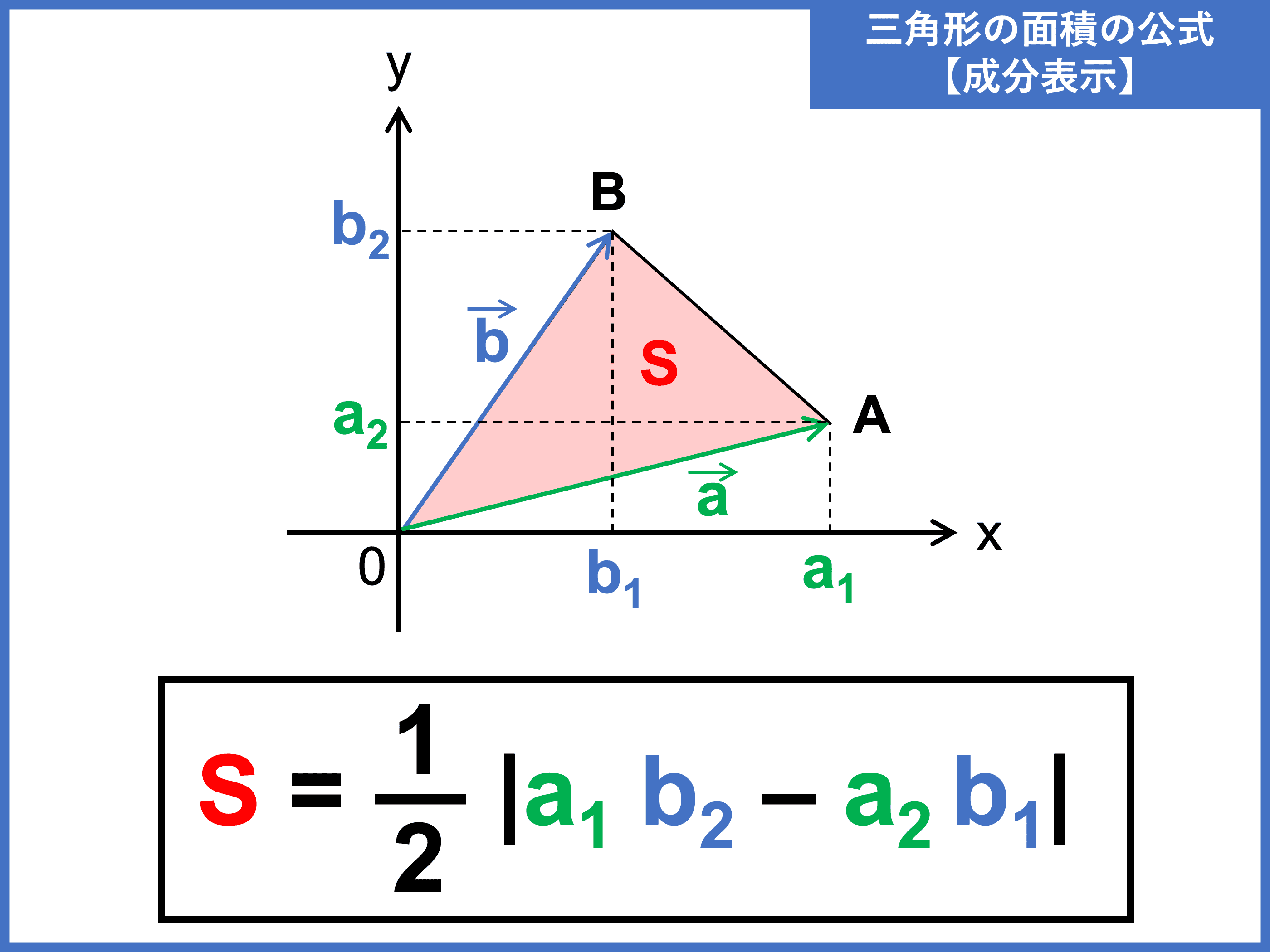



三角関数 面積 公式 証明



011 7 49 大学受験完全個別指導予備校 実力養成会 The Ability Training School 実力養成会について 学習システム 費用 ニュース ブログ 実力養成会を選んだ理由 実力養成会の考え方 講師紹介 実績 よくあるご質問 ニュース ブログ ホーム ニュース



0 件のコメント:
コメントを投稿